Robot Learning from Failures
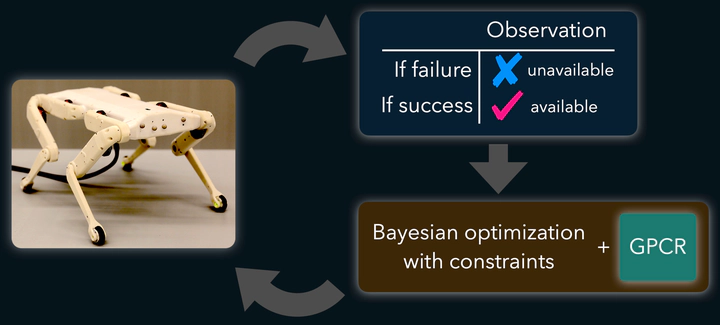 Figure 1
Figure 1During the past decade, machine learning has proven useful in making robots learn safely with data-driven algorithms. Most of this research is motivated by safety-critical applications, where a robot failure can be very costly. However, there exist a wide range of applications in which failing is not catastrophic, and could be afforded in exchange of gaining insight about what should be avoided. For example, when designing and manufacturing commercial power drills, breaking a few drill bits, throughout the learning process, is an affordable loss in exchange of learning the optimal drilling parameters.
In this project, we treat failures as an additional learning source, and develop optimization algorithms that allow failures only when the information gain is worth the cost. Because these novel algorithms do not avoid failures at all cost, they resort to less conservative strategies than existing safe learning algorithms. This enables a more global exploration with the potential of discovering multiple promising safe areas.
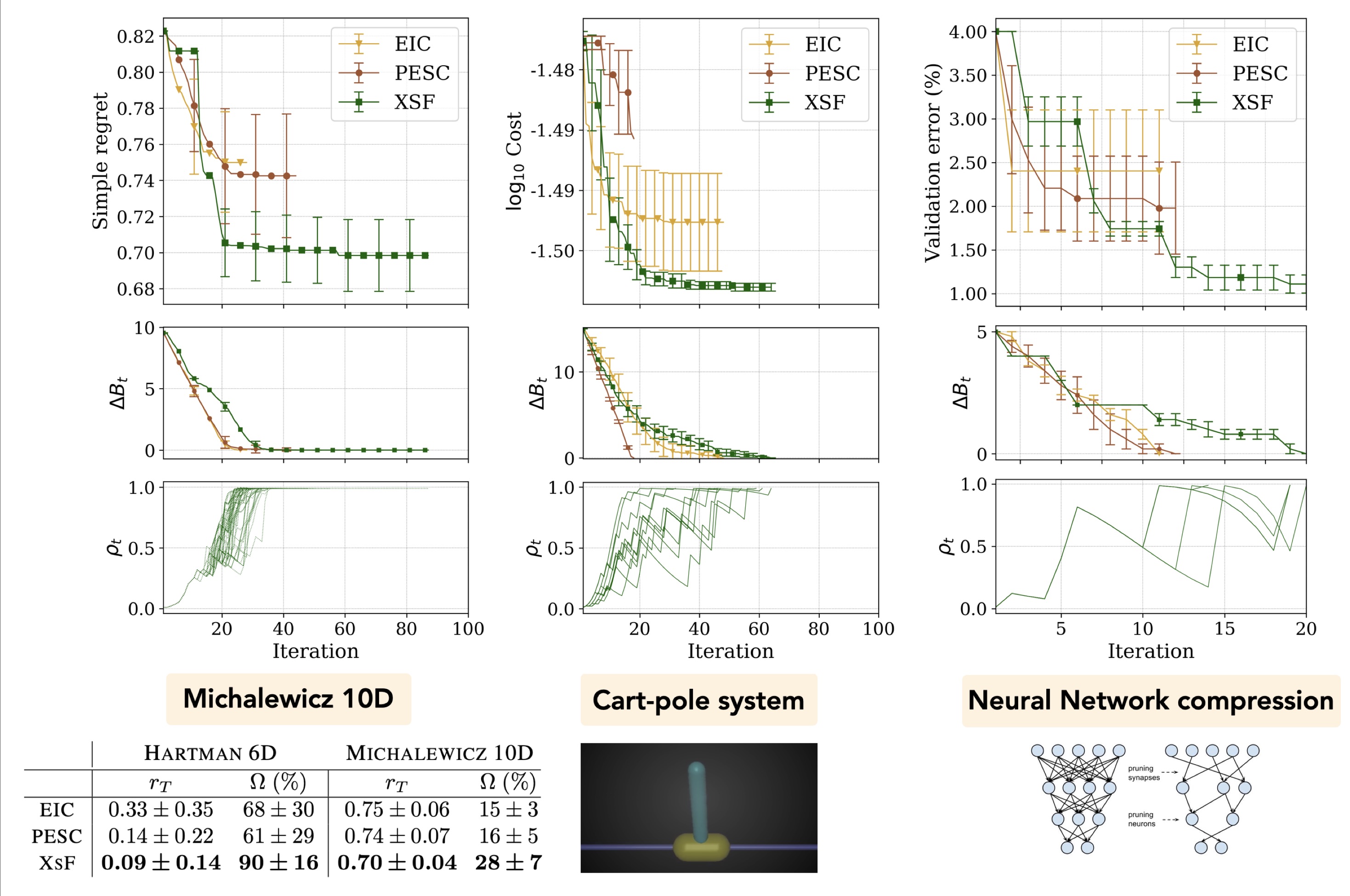
To this end, we propose in [1] an algorithm for Bayesian optimization with unknown constraints (BOC) that takes as input a budget of failures. Hence, the algorithm tries to solve the following question: given the budget of failures B, and a finite number of evaluations, make the most out of B to find the constrained optimum. Our results, in numerical benchmarks and real-world applications, show that this method achieves consistently lower regret than popular BOC methods after having exhausted the budget of failures.
In [2], a quadruped learns to jump as high as possible using Bayesian optimization with unknown constraints (BOC). Excessive current demands shut down the motors as a security mechanism, which makes the robot crash. To address this problem, BOC takes care of never revisiting areas with high probability of failure, once these are revealed. Moreover, this particular method mitigates the need of expert knowledge by automatically learning the constraint threshold, alongside with the constraint itself. This is realized by modeling the constraint using an approximate Gaussian process model (GPCR) that handles a hybrid dataset with real values and discrete labels. Our results outperform manual tuning, while also achieving the best trade-off between performance and safety as compared to state-of-the-art BOC algorithms. The research video below illustrates our proposed algorithm.
References
[1] A. Marco, A. von Rohr, D. Baumann, J.M. Hernández-Lobato, and S. Trimpe, Excursion Search for Constrained Bayesian Optimization under a Limited Budget of Failures
[code] [paper]
[2] A. Marco, D. Baumann, M. Khadiv, P. Hennig, L. Righetti, and S. Trimpe, Robot Learning with Crash Constraints, IEEE Robotics and Automation Letters (RA-L), Feb. 2021, (Submitted)
[code] [paper]