Increasing Data Efficiency in model-based RL via Informed Probabilistic Priors
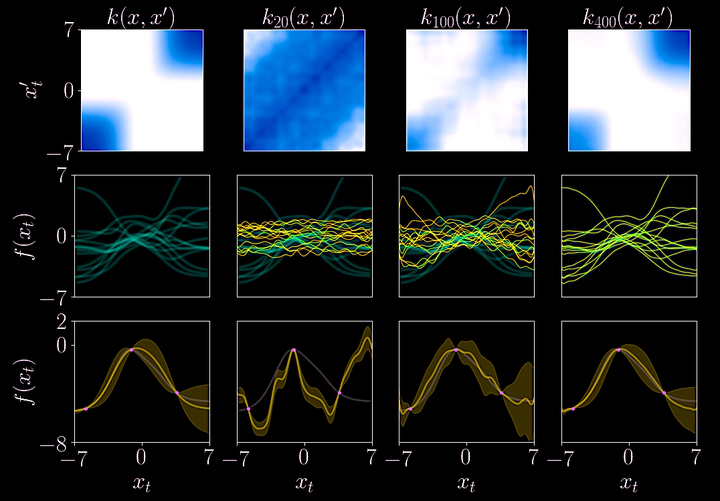 Figure 1
Figure 1Even though GPs and BNN are universal function approximators, they are hindered by low learning rates when the hypothesis space of the prior is too wide. This can be mitigated by injecting structure or information into the prior, hence shrinking the hypothesis space and increasing such learning rates. For certain dynamical systems, like walking robots, we usually have access to some form of information about the rigid body dynamics, e.g., first principles dynamical equations or high fidelity simulators. In the following, I describe two projects where I have explored these ideas.
LQR kernel design for automatic controller tuning
Designing informed kernels for learning dynamical systems
In [2], the goal is to represent a nonlinear dynamical system using multi-output Gaussian process with an informed kernel. Such kernel is constructed using simulated state trajectories by means of the Fourier transform of the dynamics. The resulting model captures the dynamics of the simulator, while also providing an explicit representation of the epistemic uncertainty about the true dynamics. Our experiments show that this kernel helps to mitigate the “sim2real” gap, while outperforming standard kernels that are not informed with the dynamics.
The kernel is constructed using a set of features, which are nonlinear mappings from Fourier domain to the state space domain. We need an increasing number of features to meaningfully represent the sought kernel. We illustrate this in Fig. 1 (top row) where the a groundtruth kernel of a scalar system is reconstructed from simulated system draws. As the number of features increases, the sampled functions are better captured (middle row). When such kernel is used for GP regression, the larger the number of features, the better is the GP able to capture the true function (bottom row).
References
[1] On the Design of LQR Kernels for Efficient Controller Learning
A. Marco, P. Hennig, S. Schaal, and S. Trimpe
Proceedings of the 56th IEEE Annual Conference on Decision and Control (CDC), Dec. 2017, pp. 5193–5200
[paper] [presentation]
[2] Out of Distribution Detection via Domain-Informed Gaussian Process State Space Models
A. Marco, Elias Morley, Claire J. Tomlin
Proceedings of the 56th IEEE Annual Conference on Decision and Control (CDC), Dec. 2023 (under review)